LetRRR Ddenote the solid bounded by the surfaces y= x, y= x2, z= xand z= 0 Evaluate D ydxdydz 2 Let Ddenote the solid bounded below by the plane z y = 2, above by the cylinder z y2 = 4 and on the sides x= 0 and x= 2 Evaluate RRR D xdxdydz 3 Suppose R4 0 R2 p x 2 y 0 dzdydx= RRR D
Y=-x^2 haircut-• ∀x ∈ E, ∀y ∈ F, we have x ≤ y Then, ∃z ∈ R such that x ≤ z, ∀x ∈ E and z ≤ y, ∀y ∈ F Least Upper Bound Theorem Every nonempty subset S of R with an upper bound has a least upper bound (also called supremum) 12 Least Upper Bound Basic PropertiesPlot and volume of y^2z^2=1 cut by the plane y=x and x=1 in the first quadrant Close Vote Posted by 5 minutes ago plot and volume of y^2z^2=1 cut by the plane y=x and x=1 in the first quadrant I need to plot and find the volume of y^2z^2=1 cut
Y=-x^2 haircutのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
 |  | |
「Y=-x^2 haircut」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「Y=-x^2 haircut」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「Y=-x^2 haircut」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「Y=-x^2 haircut」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「Y=-x^2 haircut」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「Y=-x^2 haircut」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「Y=-x^2 haircut」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「Y=-x^2 haircut」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 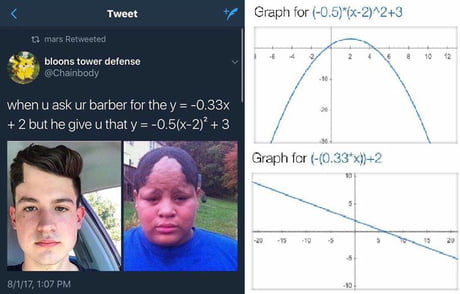 |
 |
The general solution is \frac {\tanh \left (\frac {x} {2}i c\right)} {2 x} To get it change the variable z (x)=x y (x) after that it is standard The general solution is − 2xtanh(2x −ic) To get it change the variable z(x) = xy(x) after that it is standard About Pathconnected a=1, tangent is y=3x1 and it cuts the curve again at (4,13) As slope of tangent to a curve y=f(x) is given by f'(x) or (dy)/(dx), the tangent to a curve y=f(x) at x=x_0 is (yf(x_0))=f'(x_0)(xx_0) Here we have y=x^3ax^24x3 and hence f'(x)=3x^22ax4 and hence at x=1, y=f(1)=1a43=a and f'(1)=32a4=2a1 and equation of tangent is ya=(2a1)(x1) or





0 件のコメント:
コメントを投稿